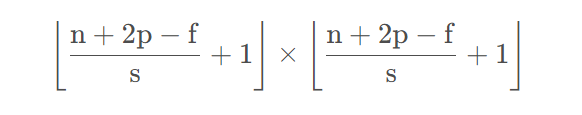CNN
CNN基础
计算机视觉
图像分类(Image Classification)
目标识别(Object detection)
神经风格转换(Neural Style Transfer)
使用传统神经网络处理机器视觉的一个主要问题是输入层维度很大。如果图片尺寸较大,例如一张1000x1000x3的图片,神经网络输入层的维度将达到3百万,使得网络权重W非常庞大。这样会造成两个后果,一是神经网络结构复杂,数据量相对不够,容易出现过拟合;二是所需内存、计算量较大。解决这一问题的方法就是使用卷积神经网络(CNN)。
CNN做的事情其实是,来简化这个neural network的架构,我们根据自己的知识和对图像处理的理解,一开始就把某些实际上用不到的参数给过滤掉,我们一开始就想一些办法,不要用fully connected network,而是用比较少的参数,来做图像处理这件事情,所以CNN其实是比一般的DNN还要更简单的。
卷积操作:以边缘检测举例
(Edge Detection)
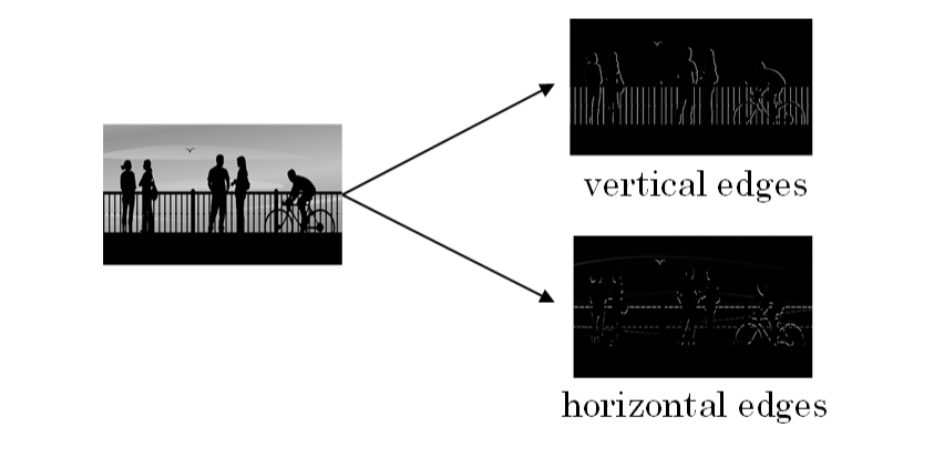
图片边缘检测的方式
- 垂直边缘检测(Vertical edges)
- 水平边缘检测(Horizontal edges)
边缘检测通过相应的滤波器(卷积核)卷积实现。
【示例】垂直检测
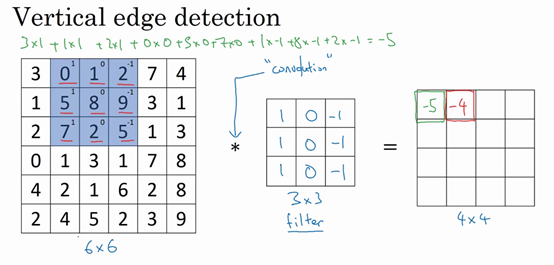
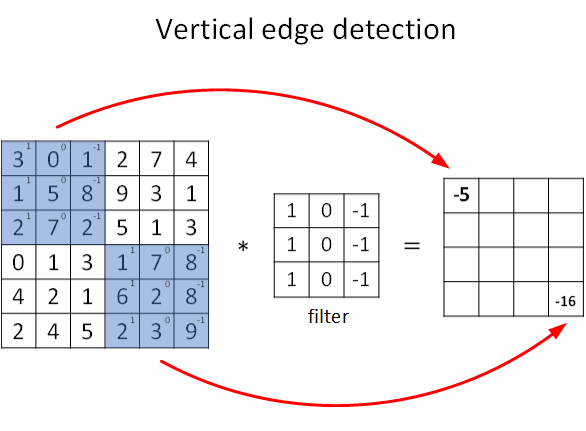
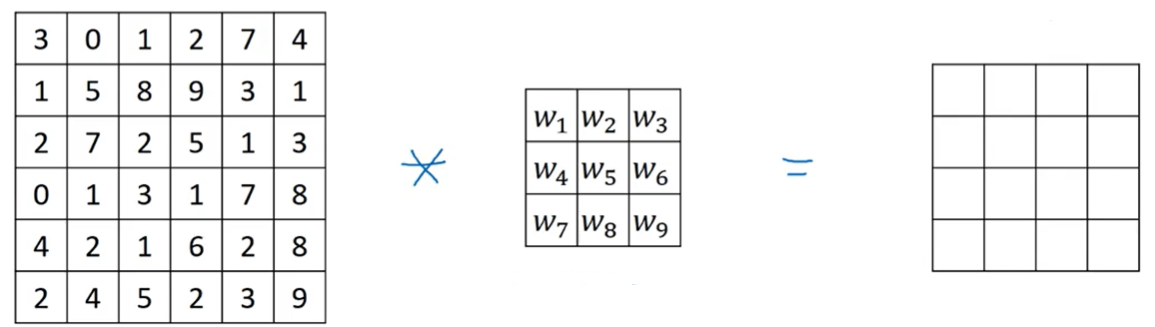
图片的边缘检测可以通过与相应滤波器进行卷积来实现。以垂直边缘检测为例,原始图片尺寸为6×6,滤波器filter尺寸为3×3,卷积后的图片尺寸为4×4
其中 *****代表卷积 上图只显示了卷积后的第一个值和最后一个值,其余值可自行计算。
边缘检测补充
图像边缘有两种渐变方式,一种是由明变暗,另一种是由暗变明。以垂直边缘检测为例,下图展示了两种方式的区别。实际应用中,这两种渐变方式并不影响边缘检测结果,可以对输出图像取绝对值操作,得到同样的结果。
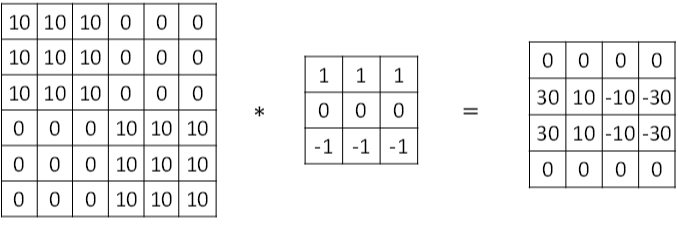
下图展示一个水平边缘检测的例子:
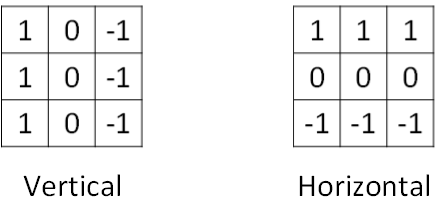
垂直边缘检测和水平边缘检测的滤波器算子如下所示:
除了上面提到的这种简单的Vertical、Horizontal滤波器之外,还有其它常用的filters,例如Sobel filter和Scharr filter。这两种滤波器的特点是增加图片中心区域的权重。(下图展示的是垂直边缘检测算子,水平边缘检测算子只需将上图顺时针翻转90度即可。)
在深度学习中,如果我们想检测图像的各种边缘特征,而不仅限于垂直边缘和水平边缘,那么 filter 的数值一般需要通过模型训练得到,类似于标准神经网络中的权重 w ww 一样由反向传播算法迭代求得。CNN的主要目的就是计算出这些 filter 的数值。确定得到了这些 filter 后,CNN浅层网络也就实现了对图片所有边缘特征的检测。
Padding
按照我们上面讲的图片卷积,如果原始图片尺寸为 n × n,filter尺寸为 f × f,则卷积后的图片尺寸为 ( n − f + 1 ) × ( n − f + 1 ) ,注意 f 一般为奇数。这样会带来两个问题:
- 卷积运算后,输出图片尺寸缩小
- 原始图片边缘信息对输出贡献得少,输出图片丢失边缘信息
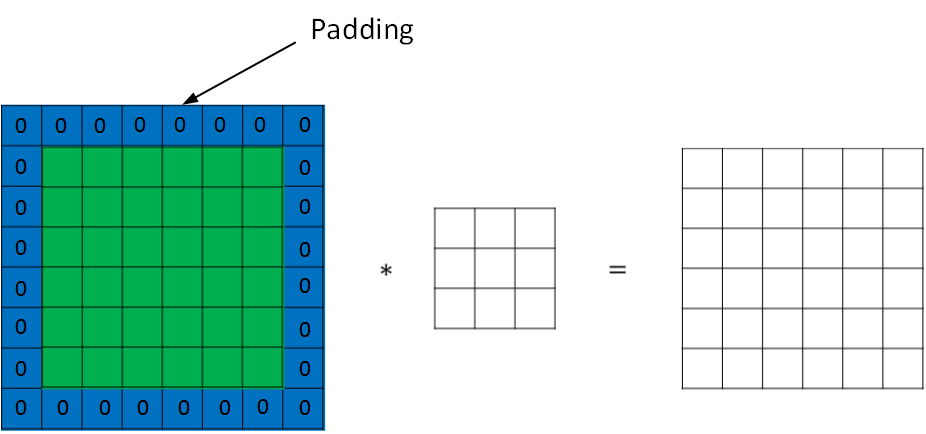
为了解决图片缩小的问题,可以 使用padding方法,即把原始图片尺寸进行扩展,扩展区域补零,用 p pp 来表示每个方向扩展的宽度。
经过padding之后:
| 原始图像padding后尺寸 | filter尺寸 | 卷积后的图像尺寸 |
|---|---|---|
| ( n + 2 p ) × ( n + 2 p ) | f × f | ( n + 2 p − f + 1 ) × ( n + 2 p − f + 1 ) |
稍作总结:
- 无padding操作,p = 0,我们称之为 Valid convolutions (不填充)
- 有padding操作,$\ p=\frac{f-1}{2}$我们称之为 Same convolutions (填充,输入输出大小相等)
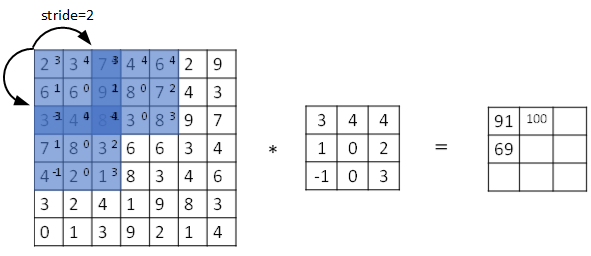
卷积步长
我们用s 表示stride长度,p 表示padding长度,如果原始图片尺寸为 n × n,filter(卷积核)尺寸为 f × f ,则卷积后的图片尺寸为:
注:商不是整数的情况下,向下取整
数学上卷积与人工智能卷积的区别:
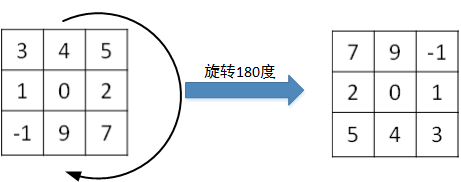
- 数学意义上的卷积(convolutions))运算会先将filter绕其中心旋转180度,然后再将旋转后的filter在原始图片上进行滑动计算。filter旋转如下所示:
- 人工智能意义上卷积:相关系数(cross-correlations)的计算过程则不会对filter进行旋转,而是直接在原始图片上进行滑动计算。
总的来说,忽略旋转运算可以大大提高CNN网络运算速度,而且不影响模型性能。
注:卷积运算服从结合率不服从交换律
三维卷积
同二维卷积多了一个维度
卷积核 channel(深度/通道数)与输入特征层 的channel 相同
输出的特征矩阵channel与卷积核个数相同
(Convolutions over volumes)
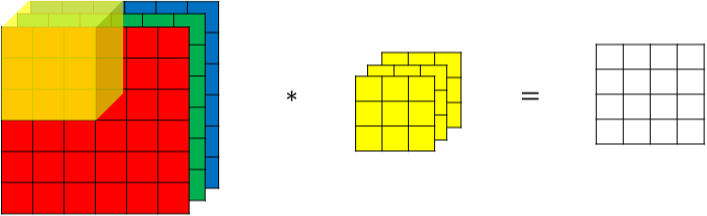
对于3通道的RGB图像,其对应的滤波器算子同样也是3通道的。例如一个图像是6 x 6 x 3,分别表示图像的高度(height)、宽度(weight)和通道(channel)。
3通道图像的卷积运算与单通道图像的卷积运算基本一致。过程是将每个单通道(R,G,B)与对应的filter进行卷积运算求和,然后再将3通道的和相加,得到输出图像的一个像素值。
不同通道的滤波算子可以不相同。例如R通道filter实现垂直边缘检测,G和B通道不进行边缘检测,全部置零,或者将R,G,B三通道filter全部设置为水平边缘检测。
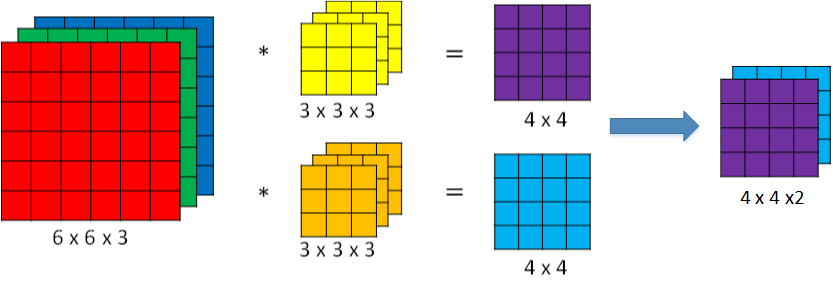
为了实现更多边缘检测,可以增加更多的滤波器组,进行多个卷积运算。例如设置第一个滤波器组实现垂直边缘检测,第二个滤波器组实现水平边缘检测。这样,不同滤波器组卷积得到不同的输出,个数由滤波器组决定。
单层卷积网络
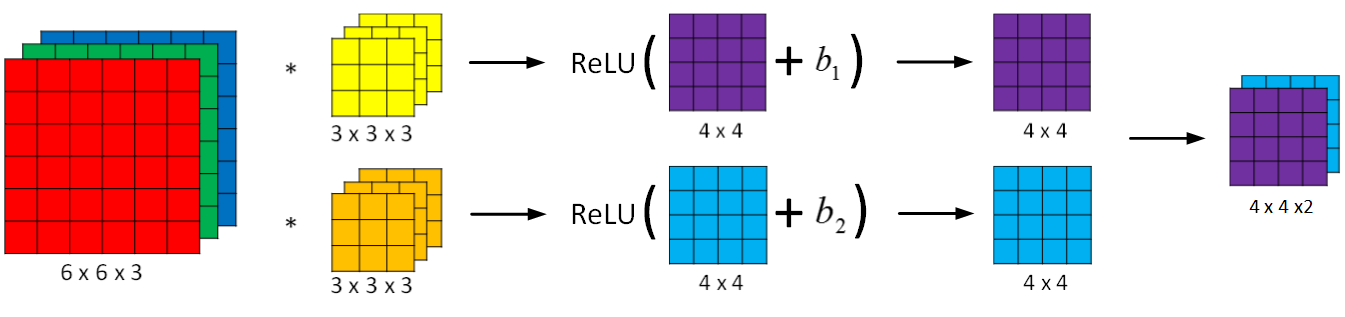
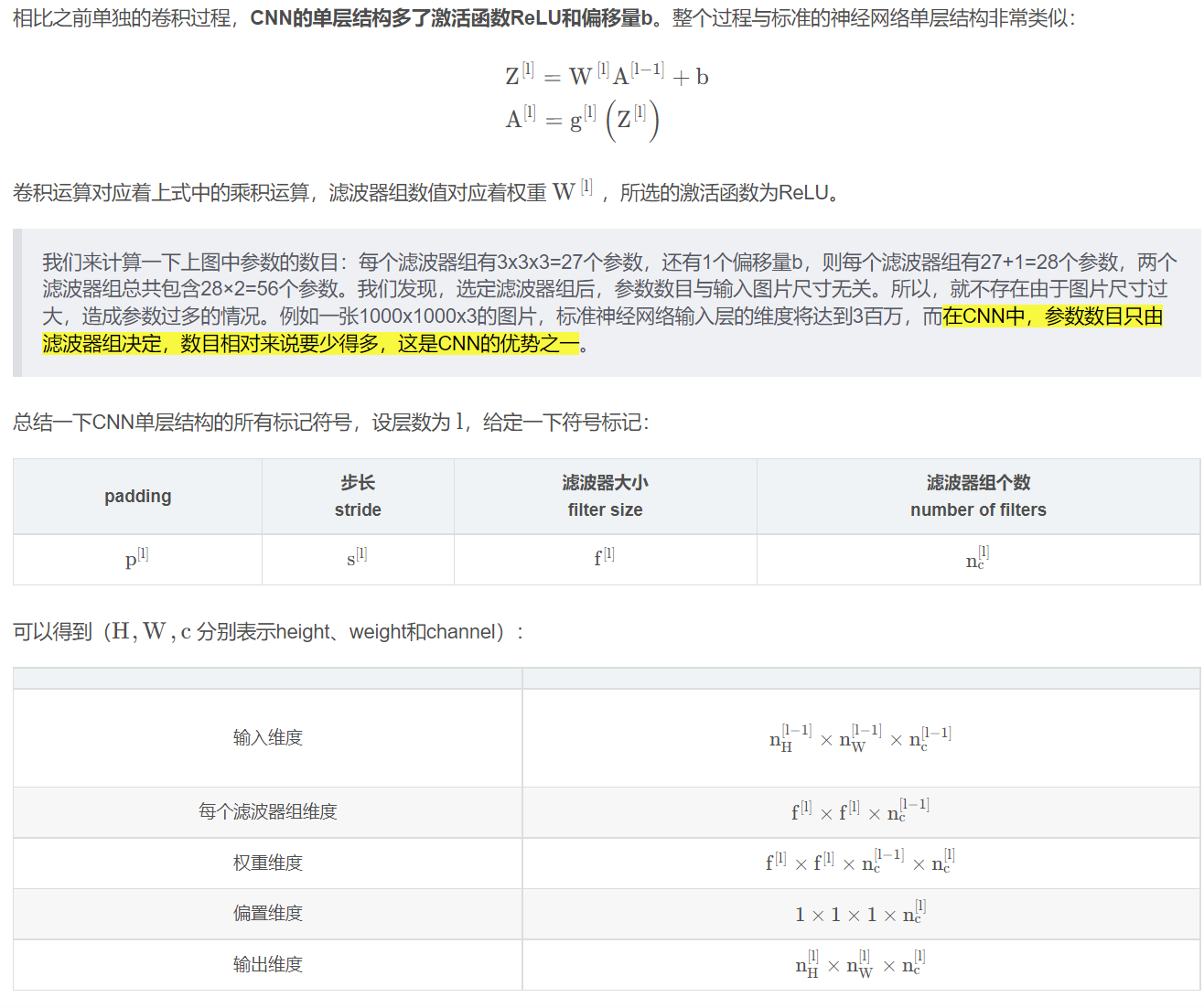
卷积神经网络的单层结构如下所示:
总结