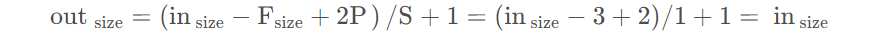VGG理论结构

VGG详解

VGG 在2014年由牛津大学著名研究组 VGG（Visual Geometry Group）提出，斩获该年 ImageNet 竞赛中 Localization Task（定位任务）第一名和 Classification Task（分类任务）第二名。
原论文地址：Very Deep Convolutional Networks for Large-Scale Image Recognition

VGG网络的创新点：通过堆叠多个小卷积核来替代大尺度卷积核，可以减少训练参数，同时能保证相同的感受野。
论文中提到，可以通过堆叠两个3×3的卷积核替代5x5的卷积核，堆叠三个3×3的卷积核替代7x7的卷积核。

CNN感受野

在卷积神经网络中，决定某一层输出结果中一个元素所对应的输入层的区域大小，被称作感受野（receptive field）。
通俗的解释是，输出feature map上的一个单元 对应 输入层上的区域大小。

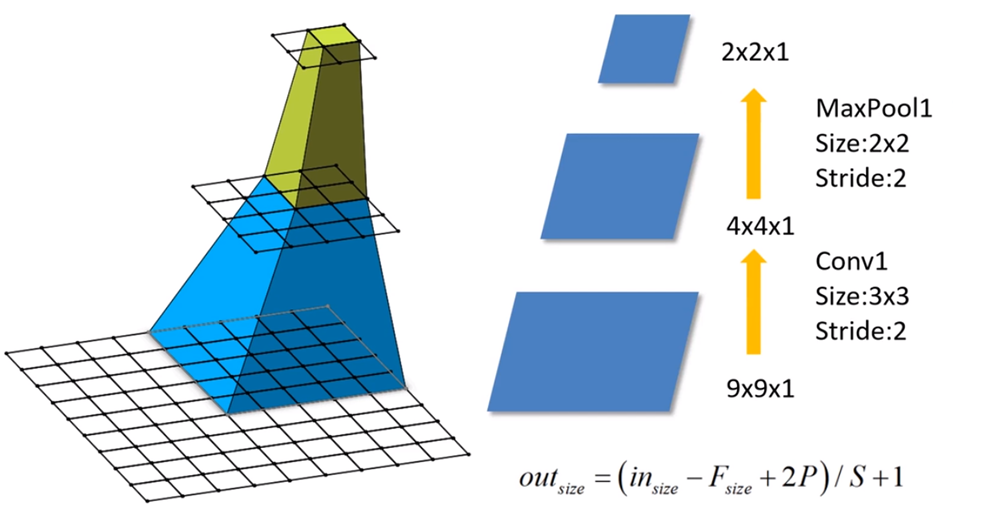
以下图为例，输出层 layer3 中一个单元 对应 输入层 layer2 上区域大小为2×2（池化操作），对应输入层 layer1 上大小为5×5
（可以这么理解，layer2中 2×2区域中的每一块对应一个3×3的卷积核，又因为 stride=2，所以layer1的感受野为5×5）
在这里插入图片描述
感受野的计算公式为：
F(i)=(F(i+1)−1)×Stride +Ksize

  • F(i) 为第 i 层感受野
  • Stride 为第 i 层的步距
  • Ksize 为 卷积核 或 池化核 尺寸

即为：下层感受野=（上层感受野-1）*步距+卷积核尺寸

以上图为例：

  • Feature map: F ( 3 ) = 1
  • Pool1：F ( 2 ) = ( 1 − 1 ) × 2 + 2 = 2
  • Conv1: F ( 1 ) = ( 2 − 1 ) × 2 + 3 = 5

小卷积核

现在，我们来验证下VGG论文中的两点结论：

1.堆叠两个3×3的卷积核替代5x5的卷积核，堆叠三个3×3的卷积核替代7x7的卷积核。替代前后感受野是否相同？

（注：VGG网络中卷积的Stride默认为1）

  • Feature map: F = 1 F=1F=1
  • Conv3x3(3): F = ( 1 − 1 ) × 1 + 3 = 3
  • Conv3x3(2): F = ( 3 − 1 ) × 1 + 3 = 5 （5×5卷积核感受野）
  • Conv3x3(1): F = ( 5 − 1 ) × 1 + 3 = 7 （7×7卷积核感受野）

2.堆叠3×3卷积核后训练参数是否真的减少了？

注：CNN参数个数 = 卷积核尺寸×卷积核深度 × 卷积核组数 = 卷积核尺寸 × 输入特征矩阵深度 × 输出特征矩阵深度
现假设 输入特征矩阵深度 = 输出特征矩阵深度 = C

  • 使用7×7卷积核所需参数个数：$ 7×7×C×C=49C^2$
  • 堆叠三个3×3的卷积核所需参数个数：$3×3×C×C+3×3×C×C+3×3×C×C=27C^2$

VGG-16

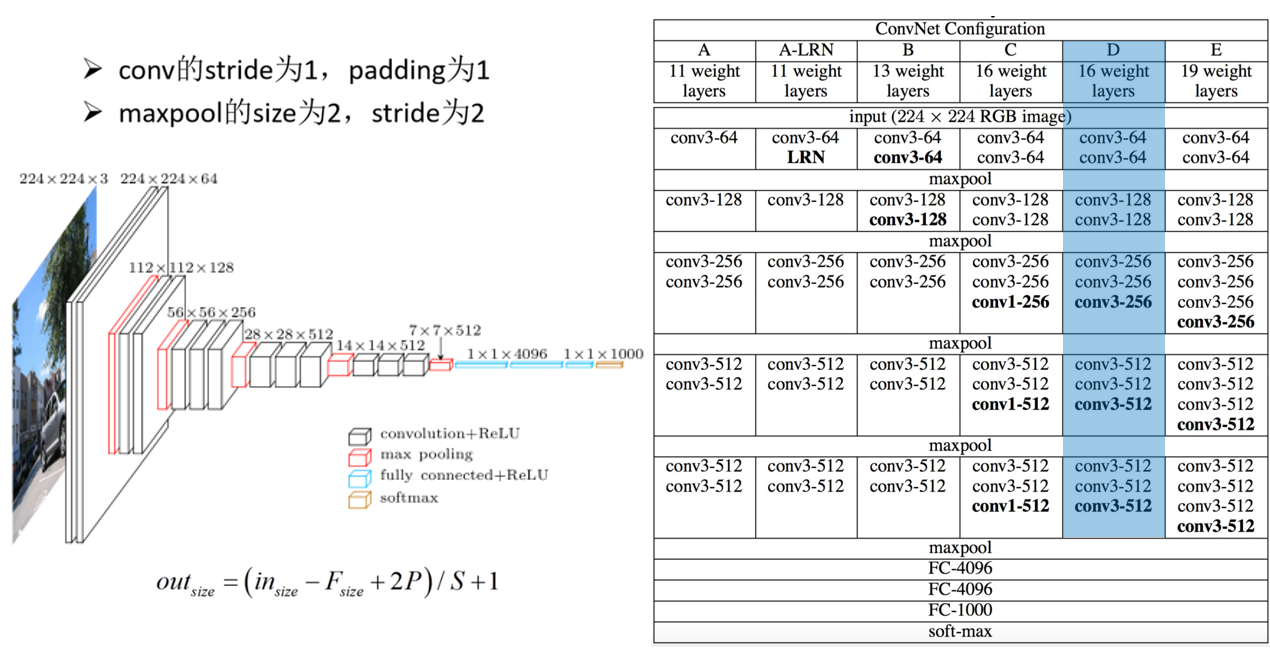
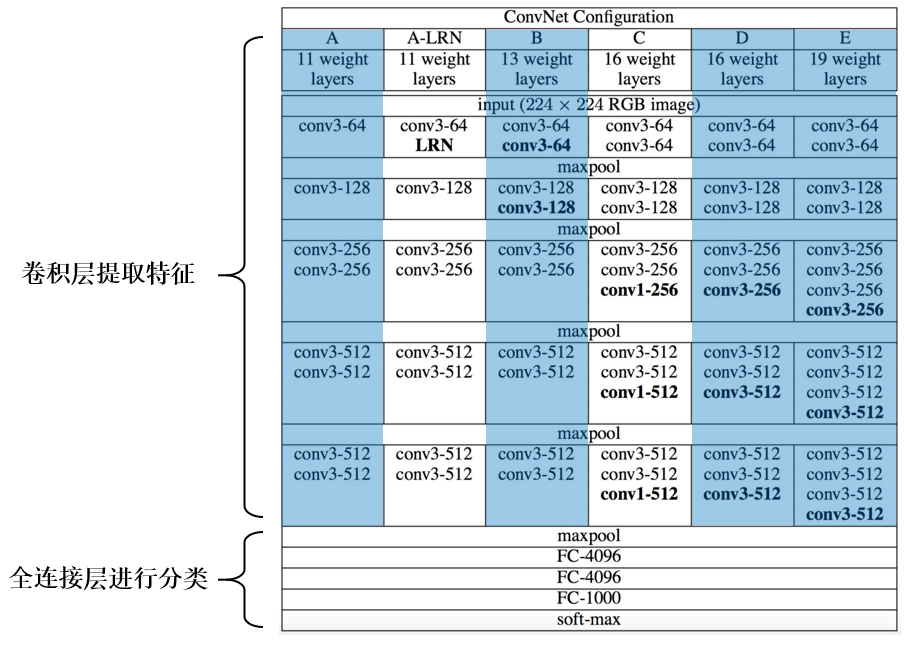
VGG网络有多个版本，一般常用的是VGG-16模型，其网络结构如下如所示：
在这里插入图片描述

图中是针对D层来写的

稍作计算可以发现，经3×3卷积的特征矩阵的尺寸是不改变的：

在这里插入图片描述

VGG-16网络，其参数多达1亿3千万，模型更加复杂一些，一般情况下，其CONV layer和POOL layer设置如下：

  • CONV = 3×3 filters, s = 1, same
  • MAX-POOL = 2×2, s = 2

在这里插入图片描述